Stan(MCMC サンプリング)を使ったクラウドサービスセットアップ時間の推定

サイボウズ・ラボの中谷です。

先日、このブログでインフラチームの湯谷さんが R と統計の社内勉強会での資料を公開する記事を書いていましたが、同じくその社内勉強会で行ったクラウドサービスのデプロイ時間を分析したお話をします。 blog.cybozu.io

5分で使えるクラウドサービス

サイボウズでは cybozu.com というクラウドサービスを展開しています。 クラウドサービスといえば「申し込んですぐ使える」のが一般的なイメージでしょう。 cybozu.com も web サイトから申し込むと、5～10分でサービスが利用可能になります。

これを実現するために、インフラ担当者が24時間待機しておき、申し込みの通知を受付けたらデータベースを切って、サービスインスタンスに申し込まれたアプリケーションをデプロイして……なんてことをしていたら担当者がすぐに倒れてしまうので、そこのところは当然自動化されています。 申し込みからサービス利用可能となるまでに段階がいくつかあるのですが、特にサービスをセットアップするタスクを担うのが、社内で "village" と呼ばれるシステムです。

village がセットアップするサービスは多岐にわたるのですが、代表的なものは次の5つになります。

• kintone
• サイボウズ Office
• サイボウズ ガルーン (garoon)
• メールワイズ (mailwise)
• セキュアアクセス (skylab)

上の4つはサイボウズの主力製品たちです。 ひとつひとつどんなサービスか説明してもいいのですが、本題ではないので泣く泣くあきらめることにします。

最後の「セキュアアクセス」は、クライアント証明書によるアクセスを提供するプロキシサービスです。 kintone など他のサービスと一緒に利用することで、それらへの安全な接続を確立します。 社内のコードネームでは "skylab" と呼ばれています。

「セキュアアクセス」だけサービスの内容を説明したのは、それが分析の動機と関係するからなのですが、それは後ほど。

手始めに重回帰！

サイボウズの R と統計の社内勉強会は輪講が中心なのですが、時にはデータやお題を持ち寄って、どのような分析をするとおもしろいか議論をすることもあります。

あるとき、village の担当であるインフラチームの内田さんが village のジョブ実行履歴を持ってきました。 それぞれのサービスごとにそれを追加するとセットアップ時間がどれくらい伸びるのか分析できないか、とのことです。

village の履歴データは次のような形をしています。 実際にはもうちょっといろいろフィールドが付いていましたが、必要なところだけに絞っています。

あ。 「R と統計の社内勉強会」なので、使うのはもちろん R です。 と言いながら、Excel や Python を使うこともちょいちょいありますが(笑)。

> head(village)
    jtime kintone garoon office mailwise skylab
1  3.6307       1      0      0        0      0
2 18.1070       0      0      0        1      0
3 13.5170       0      0      1        0      0
4 13.3591       1      0      0        0      1
5  8.7739       0      0      1        0      0
6  2.8032       1      0      0        0      0

jtime はそのセットアップジョブの実行時間（秒）、kintone から skylab まではそれぞれのサービスがセットアップ対象(=1)か、対象外(=0)かを表しています。

そのような課題とデータがあれば、真っ先に思いつくのはやはり重回帰分析でしょう。 R なら lm 関数で簡単に試してみることができます。

> summary(lm(jtime ~ 1+kintone+garoon+office+mailwise+skylab, data=village))

Call:
lm(formula = jtime ~ 1 + kintone + garoon + office + mailwise + skylab, 
    data = village)

Residuals:
    Min      1Q  Median      3Q     Max 
-21.525  -2.746  -1.746   2.254  86.841 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   4.2244     0.1172   36.04   <2e-16 ***
kintone       1.5214     0.1245   12.22   <2e-16 ***
garoon       31.1726     0.1518  205.32   <2e-16 ***
office        6.7723     0.1223   55.37   <2e-16 ***
mailwise      8.4679     0.1480   57.20   <2e-16 ***
skylab        5.3662     0.1781   30.13   <2e-16 ***

この分析結果から、係数(Coefficients) の 推定(Estimate) の項を見ると、

• 切片(Intercept)、つまり kintone から skylab までが全部 0 のときのベースの秒数が 4.2 秒かかる
• kintone を含めると 1.5秒、garoon を含めると 31.2 秒、……、skylab を含めると 5.4 秒追加される

ということがわかります。 例えば、office と skylab(セキュアアクセス) をセットアップするときは 4.2 + 6.8 + 5.4 = 16.4 秒がジョブ実行にかかる平均的な秒数となります。 実際には常にピッタリ 16.4 秒ということはなく、さらにここにノイズが足されることで散らばりが表現されます。

一番速いのは kintone です。 kintone は cybozu.com の一番人気なので、kintone がセットアップされることを前提とした特別な高速化を行っています。 そのことが、kintone のジョブ時間がとても小さいという結果に表れています。

一方、ガルーン(garoon)のセットアップは一番長い時間がかかっています。 5つの中で最も大規模なサービスなので、しかたのないところもあります。 現状は 5～10分の公約を守れていますが、お客さんが増えて負荷が高くなったとき、真っ先に高速化を求められることになりそうです。

このように、わかりやすくて「それっぽい」結果が出ました。 満足してここで終わりにしても良かったのですが、この結果を見て内田さんがつぶやきました。

「 skylab、意外と時間かかってるなー」と。

セキュアアクセス(skylab) は特別に高速な理由がある kintone についで2番目の速さですから、決して遅いわけではありません。 しかし数字を見ると、office に近い時間がかかっているようです。

サイボウズ Office はサイボウズの最も基本的なグループウェア製品で、機能てんこ盛りのアプリケーションです。 一方 skylab は、先ほど説明したように「クライアント証明書によるアクセスを提供するプロキシサービス」という単機能のアプリケーションです。 それらのセットアップに同等の時間がかかっているという分析結果が出た場合、考えられる解釈の可能性は2つです。

• 分析は正しい。skylab のセットアップがアプリケーション規模に見合わないということは、高速化できる余地が大きいはず。
• 直感（事前知識）の方が正しい。何らかの理由があって、間違った分析結果が出てしまっている。

モデルの仮定を見直す

skylab のセットアップ時間の分析結果に疑問が出てきてしまったので、それを確かめたいところです。

一番オーソドックスなアプローチは、village の履歴で「skylab のみのセットアップ」というジョブを抽出して、そのジョブ時間の分布を確認するというものでしょう。 しかし残念なことに、ここで skylab の「クライアント証明書によるアクセスを提供するプロキシサービス」という特性がそれを邪魔します。 つまり skylab は原則として必ず他のサービスとセットでセットアップされます。そのため、「skylab のみのセットアップ」というジョブは全体の中で 0.1% もなく、分布を確かめたくともデータが少なすぎます。

次に考えられる手としては、village の履歴に各サービスごとのセットアップ時間も出力するように変更する、というものです。 今回の問題の場合には十分妥当なアプローチでしょう。

しかし同様の問題で、こうしたデータの内訳を必ずしも集められないこともあるでしょう。 またこれまで集めたデータが無駄になり、新たに集めなおさなければならない（満足な分析ができるのは当分先）という問題もあります。 「上のような分析結果が出たから、明日の会議で skylab セットアップの高速化を提案します」みたいな先走りを止めるには間に合いません。

そこで、分析に使ったモデルを見なおすことを考えてみます。 重回帰は、説明変数(今回の場合 kintone や skylab)に重みとなる係数がついて足し算したところにノイズが乗っかって目的変数(今回は jtime)が得られるというモデルです。 数式で書くと次のようになります。

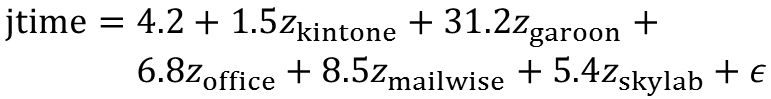
これを見ると、今回の課題に重回帰を当てはめる問題点が浮かび上がってきます。

まず、この式は、kintone や garoon の有無に寄らず共通のノイズが乗ることを表しています。 しかし、平均で 1.5 秒の重みの kintone と、31.2 秒の garoon に同じ大きさのノイズが乗ってしまうのはおかしいです。 実際には kintone の分散は garoon よりずっと小さいでしょう。

また詳しく述べませんが、分析結果の残差(Residuals)を見ると、ノイズ ε の大体の形がわかります。 ここでは、ε は最小で -21.5 という値を取りうるということだけ読み取っておきます。 すると「kintone のみセットアップ」などの場合には jtime が負の値になりうるわけです。これもまずい。

この2つの問題点を解消するために、

• 各サービスのセットアップ時間は、それぞれ独自の平均・分散を持つ、非負の確率分布に従う
• jtime はそれらの確率分布のサンプルの合計に従う

というモデルを考えることにします。

「非負の確率分布」に何を使うかを考えるために、実際に「各サービスのセットアップ時間」がどのような形の分布をしているかを見たいところです。 「mailwise のみセットアップ」というデータはそれなりの件数があるので、そのジョブ実行時間の分布を描いてみました。

library(ggplot2)
library(dplyr)
mwonly <- village %>% filter(kintone==0, garoon==0, office==0, mailwise==1, skylab==0)
ggplot(mwonly, aes(jtime, y=..density..)) +
  geom_histogram(binwidth=1, alpha=0.5) +
  geom_density() + xlim(5,30)

少々多峰性があるところは目をつぶると、「右に少し長い裾を持つ釣り鐘型の分布」であることがわかります。 そうした分布をモデリングするものはいくつか考えられますが、代表的なものとして対数正規分布（対数が正規分布に従う分布）があげられます。

jtime の対数の平均と標準偏差を対数正規分布のパラメータとする、というモーメント法ですらないアバウトなフィッティングですが、それを先ほどの分布に重ねてみました。

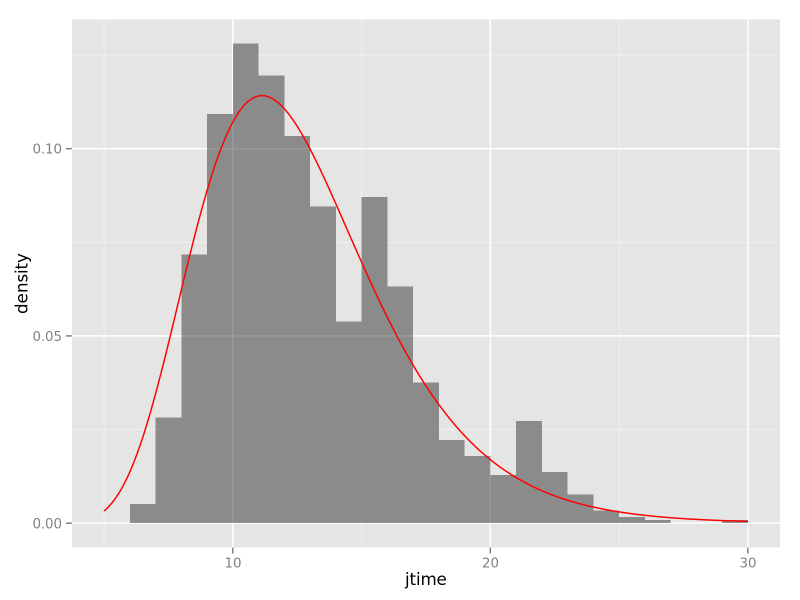
赤い線が対数正規分布なのですが、なかなかよく当てはまってくれそうです。これを使うことにしましょう。

こうして考えたモデルを図にすると次のようになりました。

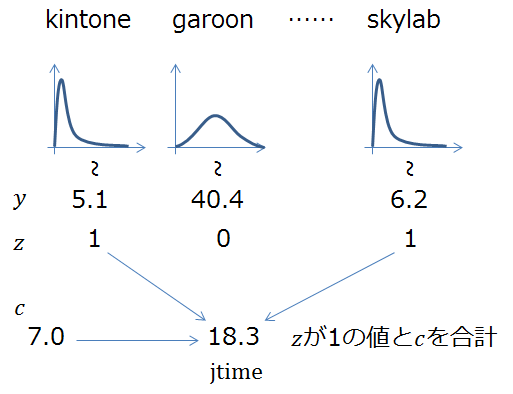
y は各サービスをセットアップした場合の時間で、それぞれ個別のパラメータを持つ対数正規分布に従います。 実際には全ての y が有効なのではなく、選択したかどうか z が 1 である y のみを合計、それに重回帰の切片に相当する定数の c を加えたものが jtime となる、というモデルです。

こうして作った「ぼくのかんがえたさいきょうのモデル」は、観測できない y を積分消去する必要があるため、一般的な最尤推定法で解くのは難しいです。 しかし、これをベイズ化すると、なんと解く方法があります。

Stan(MCMC サンプリング)を使った推論

Stan はベイズモデルをサンプリング法によって解く MCMC サンプラーです。 他にも WinBUGS や JAGS などがあります。

心苦しいですが Stan、ベイズモデル、MCMC などのキーワードの解説は省略します。 詳しくは下記の書籍などをご覧ください。

• 岩波データサイエンス vol.1
• データ解析のための統計モデリング入門

ここでは、Stan を「ふつうにやったら解けないモデルを、頑張って解いてくれるツール」として使います。 そのためには、上のモデルをベイズ化して、Stan のモデルファイルとして記述すれば OK です。

といっても、それほど難しい話ではありません。 先ほどのモデルを条件付き確率の形で書き下してあげること、そこに出てきたパラメータを確率変数と見なすこと、の2点を行えば、後は Stan のモデルファイルに逐語訳するだけです。

まず各サービスのセットアップ時間の分布からのサンプル y を条件付き分布で書くとこうなります。

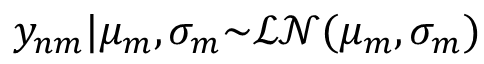
n, m はそれぞれデータ、サービスを指すインデックス、 は対数正規分布(log-normal の頭文字を取って LN と表します)のパラメータです。

次に jtime を z が 1 である y と c の合計とする部分も条件付き分布で表すのが MCMC サンプラー的には自然です（頑張ったら避けることはできるが）。そこで jtime は、その合計を中心とする小さな正規分布に従うことにします。

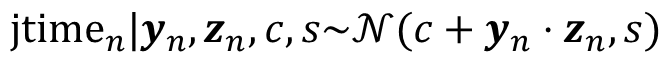
y と z の内積を取れば、ちょうど「 z が 1 である y の合計」になるので、このように簡単に書けます。

Stan のモデルファイルでは、これらの条件付き分布を次のように記述します。 見慣れない表記に戸惑うかもしれませんが、落ち着いて照らし合わせると、上の数式の逐語訳になっていることがわかるでしょう。

model {
  for (n in 1:N) {
    jtime[n] ~
      normal(c + dot_product(y[n], z[n]), s);
    for (m in 1:M) {
      y[n, m] ~ lognormal(mu[m], sig[m]);
    }
  }
}

実際には、ここに観測値を宣言する data セクション、パラメータや潜在変数を宣言する parameter セクション、そして事前分布の記述を追加することになりますが、煩雑さを避けるため省略します。

Stan の推論を R から呼び出して行わせることができる rstan というパッケージがありますので、それを使って推論した結果を可視化することができます。

library(rstan)
data <- list(N=nrow(village), M=5, jtime=village$jtime, z=village[2:6])
fit <- stan(file=stan_file, data=data)
traceplot(fit, pars=c("mu","c"))

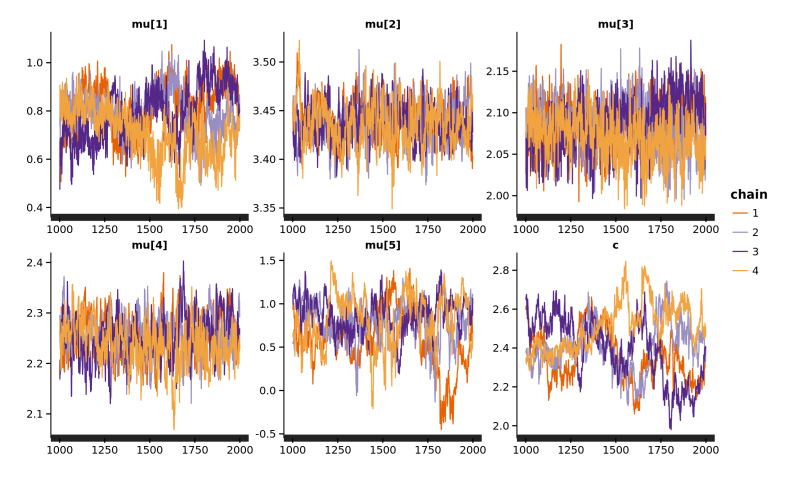
これはサンプルの系列をプロットしたもので、MCMC サンプラーではこのプロットから分布の収束具合を確認するのが一般的です。 プロットの色は初期値を変えて4回の系列を取り直したものに対応しています。4つのギザギザが安定かつきれいに重なっていたら「収束してるっぽい」と判断します（あくまでも「ぽい」であって、収束を保証するものではありません）。

それを踏まえて上のプロットを見ると…… はい、そうですね、少々不安定＆ビミョウに重なってません（汗）。 実は、上で mailwise だけの jtime の分布を見たときに多峰性があった時から覚悟していましたが、この単純なモデルでは jtime の振る舞いをモデル化しきれていないようです。

というわけで、厳密にはここでアウトですが、現実のデータはそんなにキレイじゃないんだよ！　と開き直って、この結果から推定値を引っ張り出します。 μ の系列はそれほどデタラメでもなさそうですし、大丈夫でしょう（たぶん）。

重回帰の結果と見比べるために必要なのは切片 c と y の推定値です。c の推定値は簡単に得られます。

> print(fit, pars="c")

  mean se_mean   sd 2.5%  25%  50%  75% 97.5% n_eff Rhat
c 2.41    0.04 0.15 2.13 2.31 2.41 2.52  2.69    14 1.34

MCMC サンプラーでは分布の平均を推定値とするのが一般的なので、 2.4 が c の推定値となります。

y は少々面倒です。 の推定値なら簡単だったのですが、欲しいのは の平均値なので一工夫する必要があります。

> library(reshape2)
> y <- melt(extract(fit, "y")$y, value.name="y")
> lbl <- c("kintone", "garoon", "office", "mailwise", "skylab")
> y$m <- lbl[y$Var3]
> y %>% group_by(m) %>% summarise(mean(y))

         m   mean(y)
     (chr)     (dbl)
1   garoon 31.670752
2  kintone  3.794754
3 mailwise 10.133677
4   office  8.754018
5   skylab  4.856500

間が空いてしまったので問題設定を忘れてしまったかもしれませんね（苦笑）。

重回帰の結果を見て、「 skylab の重みが大きすぎるのではないか」というのが出発点でした。 今回のベイズモデルで推定した skylab の重みは 4.9 となり、office の重み 8.8 より kintone の重み 3.8 に近い値が得られました。 この分析によれば、skylab のセットアップはそれほど遅いわけではなさそうです。よかったよかった。

まとめ

と、一段落ついたようにまとめましたが、このベイズモデルもまだまだゴールではありません。 ノイズの独立性を暗黙に仮定してしまっており、「1つのジョブで kintone のセットアップが遅いときは、対象のサーバの負荷が高いことが予想されるので、 garoon も遅いのでは？」ということを排除しています。

系列のプロットが重なっていないことも懸念点です。 おそらくは多峰性に起因するものではないかと思われますが、それを説明する変数を観測できていないので単純にモデリングはできません。 そこで未観測の外乱要因を組み込み、それごと推定するようなモデリングに発展することが考えられます。 上で挙げた参考文献「岩波データサイエンス vol.1 」「データ解析のための統計モデリング入門」では、そのようなモデリングを「個性をモデリングする階層ベイズ」として解説されています。

また実際には、このように一直線に進んだのではなく、もうちょっといろいろ試行錯誤という名の寄り道をしていました。 教科書で難しくてカッコいいモデルを見るとつい使ってみたくなりますが、いきなり複雑なモデルを「正解」として引き当てるのは、全く同じようなデータを同じように分析したことがある人だけでしょう。 現実には、やはり簡単なモデルからスタートして、そこで見つけた問題点を反映して、モデルを取り替えたり、ブラッシュアップしたり。 つまるところデータ解析は、いろいろなモデルを試して引き出しを増やしつつ、データをよく見て楽しむことが重要なのかな、と思っています。

小規模ながら現実のデータを使った、型通りではない統計解析のパターンの一つとして楽しんでもらえたなら嬉しいです。