初めに
サイボウズ・ラボの光成です。
DNN(deep neural network : 深層学習)といえばGPUや専用プロセッサを使うのが主流です。 しかしIntelはCPUで高速にDNNをするためのライブラリ MKL-DNN を提供しています。 MKL-DNNはIntelの最新CPUに対応したオープンソースソフトウェアなのでコードを見ると勉強になります。
ここではMKL-DNNで使われているテクニックをいくつか紹介します。
概要
- MKL-DNNの紹介
- Xbyakの紹介
- 呼び出し規約
- 圧縮displacement
- ReLU
- exp
- 内積 vpdpbusd
- キャッシュコントロール
想定読者
C++11とx64 CPUのアセンブリ言語の知識をある程度仮定します。 機械学習についてはその知識がなくても最適化手法が理解できるよう、最小限の説明をします。
MKL-DNNの特長
まずMKL-DNNの特長を簡単に紹介します。
- 畳み込みや内積などの最適化された基本演算
- RNN, LSTM, GRUなどのネットワークサポート
- ReLU, tanh, softmaxなどの活性化関数サポート
- 32-bit浮動小数点数と低精度int8整数をサポート
- pooling AVG/MAX, batch normalization
- 複数の種類を組み合わせられる柔軟なメモリレイアウト
個別の用語はさておき、いろいろな種類の行列計算を高速にするライブラリととらえれば十分です。 MKL-DNNはTensorFlow, Chainer, Caffeなどのより高次の機械学習ライブラリ内で使われる基本ライブラリです。 またIntelはMKL-DNNを組み込んでNumPyを高速化した Python も提供しています。
ソースファイル
MKL-DNNのIntel CPU向けに最適化されたコードは src/cpu にあります。 特にjitで始まるファイル名がAVX-512などの専用命令を使った最適化コードです。 AVX-512については AVX-512(フォーマット)詳解 などをごらんください。
Xbyak
MKL-DNNのエンジン部分は拙作の Xbyak で記述されています。 XbyakはIntelのアセンブリ言語(以下asm)命令を実行時に生成するC++のライブラリです。
次の特長があります。
- 実行時コード生成
- C++でIntel形式のasmライク命令を記述可能
- AVX-512など最新CPUの命令に対応
1番目の特長により、CPUに応じた命令の切り替えやパラメータに応じた最適なコードを実行時に生成できます。
2番目の特長はasmの擬似命令をC++の文法で記述できるという意味です。 asm自体はIntel形式に慣れた人が極力違和感がないようなインタフェースを提供しています。 アセンブリ言語の擬似命令というのは何十年も前から殆ど変わっていない古い文法、あるいは無理やり拡張した形が多く、覚えるのも書くのも大変です。 それをC++で記述できるのはとても楽で便利です。
3番目は先日発表された 第2世代Xeonスケーラブル・プロセッサ でサポートされる命令群DL Boostにも対応しています。
表記法
XbyakはIntel表記を採用しているので命令に与える引数はデスティネーション、ソースの順です。
mov(ptr[rax], rcx); // *rax = rcx; raxが指すアドレスにrcxを書き込む add(rax, rcx); // rax += rcx; vaddps(zmm2, zmm1, zmm0); // zmm2 = zmm1 + zmm0
また以下で出てくるコードではレジスタ名が直接使われるのではなく、適当な変数名にaliasされています。
auto dst = zmm2; auto src1 = zmm1; auto src2 = zmm0; vaddps(dst, src1, src2); // dst = src1 + src2
前置きが長くなりましたが、それではMKL-DNNの中身を少しずつ見ていきましょう。
関数のプロローグとエピローグ
関数のプロローグとエピローグとは関数本体の前処理の部分、後処理の部分を指します。 レジスタやスタックを設定、復元します。
呼び出し規約
MKL-DNNはLinux, macOSだけでなくWindowsにも対応しています。LinuxやmacOSの関数の呼び出し規約とWindowsの呼び出し規約は異なります。 関数の引数に渡されるアドレスや、関数から抜けるときに値の復元が必要なレジスタが異なるのです。
| 引数 | Windows | Linux |
|---|---|---|
| 1番目 | rcx | rdi |
| 2番目 | rdx | rsi |
| 3番目 | r8 | rdx |
| 4番目 | r9 | rcx |
| 退避不要 | r10, r11 | r8~r11 |
| 退避必要 | r12~r15,rdi,rsi,rbx,rbp,rsp | r12~r15,rbx,rbp,rsp |
Xbyakもこれらの差異を吸収するStackFrameクラスを提供しています。 しかしレジスタやスタックの使い方というのは用途に強く依存するので各アプリケーションが必要に応じてラッパークラスを作ることが多いです。
MKL-DNNでは jit_generator.hpp がこれらの差異を吸収しています。 abi_param1などが引数のレジスタ、abi_save_gpr_regsが退避すべきレジスタの種類を表します。
#ifdef XBYAK64 constexpr Xbyak::Operand::Code abi_save_gpr_regs[] = { Xbyak::Operand::RBX, Xbyak::Operand::RBP, Xbyak::Operand::R12, Xbyak::Operand::R13, Xbyak::Operand::R14, Xbyak::Operand::R15, #ifdef _WIN32 Xbyak::Operand::RDI, Xbyak::Operand::RSI, #endif };
preamble()で関数のプロローグで保存すべきレジスタを退避、postamble()で関数から戻るときレジスタを復元します。 AVXを使うときはpostamble()でvzeroupperを実行します。
void postamble() { ... if (mayiuse(avx) && !mayiuse(avx512_mic)) vzeroupper(); ret(); }
vzeroupperを呼ばないとこの関数の後でSSE命令を実行したときに大きなペナルティを受けます。 コンパイラは自動的にこの命令を挿入しますが自分でasmを記述するときは忘れないようにしなければなりません。
圧縮displacement
preamble()の中で
if (mayiuse(avx512_common)) { mov(reg_EVEX_max_8b_offt, 2 * EVEX_max_8b_offt); // reg_EVEX_max_8b_offt = rbp, EVEX_max_8b_offt = 0x200 }
というコードを実行し、EVEX_compress_addr()の中でオフセットに応じて何かずらした値を返しています。
... template<typename T> Xbyak::Address EVEX_compress_addr(Xbyak::Reg64 base, T raw_offt, bool bcast = false) { ... int scale = 0; if (EVEX_max_8b_offt <= offt && offt < 3 * EVEX_max_8b_offt) { offt = offt - 2 * EVEX_max_8b_offt; scale = 1; } else if (3 * EVEX_max_8b_offt <= offt && offt < 5 * EVEX_max_8b_offt) { offt = offt - 4 * EVEX_max_8b_offt; scale = 2; } auto re = RegExp() + base + offt; if (scale) re = re + reg_EVEX_max_8b_offt * scale; if (bcast) return zword_b [re]; else return zword [re]; } ...
これは何をしているのでしょうか。
x64ではメモリ操作をする命令はModR/M + SIB + displacementという形でエンコーディングします(詳細は略)。 たとえば
mov(rax, ptr[rcx + 16]); movaps(xmm0, ptr[rcx + edx * 8 + 32]);
の16や32がdisplacementです。
displacementは符号付き8bit以内なら1byte、それ以外は4byteにエンコードされます。 同じ処理をするならbyte数が短い命令の方が命令密度が高くなります。
ところがAVX-512では一つのレジスタが512bit(=64byte)なのでデータのdisplacementもその倍数になりがちです。
vaddpd(zmm0, ptr[rax + 64 * 0]); vaddpd(zmm1, ptr[rax + 64 * 1]); vaddpd(zmm2, ptr[rax + 64 * 2]); vaddpd(zmm3, ptr[rax + 64 * 3]);
そうすると従来のエンコーディングでは64 * 2や64 * 3は1byteに納まらず命令が長くなってしまいます。
そこでAVX-512では圧縮displacementというエンコーディングが導入されました。 displacementがある範囲以内では64(命令ごとに異なる)が何個分と扱うことで命令を短くするのです。 上記の例ではdisplacementに相当する部分が1byteになります。
またdisplacementは符号付きなので[0, X]の範囲よりもベースをずらして[-X/2, X/2]の方が1byteに納まる率が増えます。 このようにして全体の命令長を減らします。 たとえばrbp = 0x200のとき積和演算をする
v4fmaddps(zmm0, zmm1, ptr[rax + 64 * 32]); // 通常 v4fmaddps(zmm0, zmm1, ptr[rax + rbp * 2 + 64 * 32 - 0x400]); // オフセットずらし
は同じ処理をしますが後者の方が2byte短いです。EVEX_compress_addr()はこのようなコードを生成します。 この例に限ってはrbpをうまくとればもっと短くできますがループ内の複数の箇所で統一的に扱えるようにこの形にしているようです。
活性化関数
ニューラルネットワークでは活性化関数と呼ばれる非線形な関数が使われます。 たとえばReLUやシグモイド関数などがあります。ReLU(x)は単なるmaxなので簡単なのですがシグモイド関数は指数関数exp(x)が必要です。
ReLU
/* activation */ template <typename T, typename A, typename U = typename utils::remove_reference<T>::type> inline U relu_fwd(T s, A alpha) { return s > 0 ? s : (U)(s * alpha); }
に対応するSIMDの実装は次のrelu_compute_vector()です(読みやすさのために加工しています)。
relu_compute_vector(const Vmm &vmm_src) { const int alpha_off = 0, zero_off = 1; // vmm_srcが入力レジスタ // vmm_aux1はテンポラリレジスタ vmovups(vmm_aux1, vmm_src); ... if (isa == avx2) { vmulps(vmm_src, vmm_src, alpha_off); // vmm_src *= alpha_off vcmpgtps(vmm_mask, vmm_aux1, zero_off); // vmm_mask = vmm_aux1 > zero_off ? -1 : 0 vblendvps(vmm_src, vmm_src, vmm_aux1, vmm_mask); // vmm_src = vmm_mask ? vmm_src : vmm_aux1 } else if (isa == avx512_common) { vmulps(vmm_src, vmm_src, alpha_off); vcmpps(k_mask, vmm_aux1, zero_off, _cmp_nle_us); // k_mask = vmm_aux1 > zero_off ? -1 : 0 vblendmps(vmm_src | k_mask, vmm_src, vmm_aux1); // vmm_src = k_mask ? vmm_src : vmm_aux1 }
AVX2の場合はvcmpgtpsを使ってvmm_srcがzero_offより大きい要素に対応したvmm_maskを生成します。 vblendvpsでそのマスクに対応した要素だけ移動しています。
AVX-512ではvcmppsが拡張されて要素ごとにXより大きい値に対応するマスクレジスタk_maskを生成できるようになりました。 そして新設されたvblendmpsでk_maskに従って対応する要素を移動します。
SIMD化されたexp(x)
シグモイド関数やtanh(x)に必要なexp(x)の計算方法を紹介します。 MKL-DNNでは jit_eltwise.cpp のexp_compute_vectorがSIMD化されたexp(float x)のコードを生成します。 exp_compute_vectorを元に、理解しやすいように抽出したアルゴリズムを以下に記します。 SIMD化しやすいようテーブル引きを使わないアルゴリズムが使われています。
exp(x)の近似アルゴリズム
- exp(x) = 2x log2(e)と変形する
- y := x log2(e)についてy = n + a, nは整数, |a| ≦ 1/2となるようにnとaに分解する
- b := a log(2)とするとa = b log2(e)
- exp(x) = 2n + a = 2n・2b log2(e) = 2n・eb
- c := 2nは2の整数巾なので高速に求められる
- d := ebは|b| ≦ (1/2)log(2) = 0.346... なのでテイラー展開で近似計算する
- exp(x) = c * dを求める
exp(x)の実装
ではどのように実装しているか順に見ていきましょう。
VmmはSSE, AVX, AVX-512を切り換えるクラスです。 型に対応したSIMD命令を生成するラッパー関数が定義されています。
using Vmm = typename utils::conditional3<isa == sse42, Xbyak::Xmm, isa == avx2, Xbyak::Ymm, Xbyak::Zmm>::type; ... void jit_eltwise_injector_f32<isa>::exp_compute_vector(const Vmm &vmm_src) { // vmm_srcが入力レジスタ vminps(vmm_src, vmm_src, table_val(10)); // vmm_src = min(vmm_src, table_val(10)) vmaxps(vmm_src, vmm_src, table_val(11)); // vmm_src = max(vmm_src, table_val(11)) vmovups(vmm_aux0, vmm_src);
入力レジスタvmm_srcを最大値table_val(10)と最小値table_val(11)にクリッピングしています。 table_valの値はJIT前に設定されています(elu_prepare_table)。
vmulps(vmm_src, vmm_src, table_val(2)); // vmm_src *= log2(e) ; Step 2のy vaddps(vmm_src, vmm_src, table_val(1)); // vmm_src += 0.5
yに0.5を足してfloorをとれば四捨五入になってStep 2のnが求まります。
floorは次のようにして求めます。
if (isa == avx512_common) { vcvtps2dq(vmm_aux1 | T_rd_sae, vmm_src); // vmm_aux1 = int(vmm_srcをround down) vcvtdq2ps(vmm_aux1, vmm_aux1); // vmm_aux1 = float(vmm_aux1) #if 1 vcmpps(k_mask, vmm_aux1, vmm_src, _cmp_nle_us); vmovups(vmm_aux3 | k_mask | T_z, table_val(0)); // table_val(0) = 1 vsubps(vmm_aux1, vmm_aux1, vmm_aux3); #endif } else { vroundps(vmm_aux1, vmm_src, _op_floor); // vmm_aux1 = floor(vmm_src) }
AVXではvroundpsでfloorを計算できますがAVX-512には対応する命令がありません。 その代わりにAVX-512では整数への変換命令vcvtps2dqに丸めモードを指定できるのでマイナス無限大への切り捨て(T_rd_sae)を設定します。 結果は整数なのでvcvtdq2psでfloatに戻します。
その後に続く#if 1 ... #endifの部分は不要に見えます。試しにpull reqを出してみました。 間違ってたら後で訂正します。
少し飛ばしてStep 5の2nの処理を見ましょう。
vcvtps2dq(vmm_aux1, vmm_src); // vmm_aux1 = int(vmm_src) vpaddd(vmm_aux1, vmm_aux1, table_val(4)); // vmm_aux1 += 0x7f vpslld(vmm_aux1, vmm_aux1, 23); // vmm_aux1 <<= 23
floatのバイナリ表現をX = [s:a:b](s:1bit, a:8bit, b:23bit)とするとXが表すfloatの値は(-1)s2a-127(1+b/223)です。
したがって32bit整数として指数nに0x7f(=127)を足して左に23bitシフトするとfloatとしての2nができあがります。 簡潔でうまい方法ですね。
Step 6はテイラー展開の処理です。ここでは5次までの項を計算しています。p[i] = 1 / i!として
exp(x) = 1 + x p[1] + x2 p[2] + x3 p[3] + x4 p[4] + x5 p[5]
= 1 + x(p[1] + x(p[2] + x(p[3] + x(p[4] + x p[5]))))
なので5回の積和演算命令vfmadd213psで処理します。
// y = y * x + p4 vfmadd213ps(vmm_src, vmm_aux0, table_val(8)); // y = y * x + p3 vfmadd213ps(vmm_src, vmm_aux0, table_val(7)); // y = y * x + p2 vfmadd213ps(vmm_src, vmm_aux0, table_val(6)); // y = y * x + p1 vfmadd213ps(vmm_src, vmm_aux0, table_val(0)); // y = y * x + p0 vfmadd213ps(vmm_src, vmm_aux0, table_val(5)); //exp(q)
最後にStep 5とStep 6の値を掛けて完了です。
// y = y * 2^n
vmulps(vmm_src, vmm_src, vmm_aux1);
exp(x)のような複雑な関数を20命令以下で計算できるとはすごいですね(しかも16個同時に)。
内積
まずベクトルの内積について紹介しましょう。 DNNでは単精度浮動小数点数(float)を使っていましたが、近年精度を落としてもよいところは1バイト整数や1ビットで行うアルゴリズムが提案されています。
Intelの第二世代Xeon SP(スケーラブルプロセッサ Cascade Lake-AP)で搭載されたDL Boost(Deep Learning)命令を使うと1バイト整数ベクトルの内積を高速に求められます。
vpdpbusd命令
CPUがAVX512_VNNI命令セットに対応しているとvpdpbusdを使えます。 vpdpbusdはuint8_t u[64]とint8_t s[64]の各要素をそれぞれ符号無し整数、符号あり整数としてintに拡張し、4次元ベクトルの内積を16個並列に求めてもとのint dst[16]に足し合わせます。
この処理をCで記述すると次のようになります。
// vpdpbusd(dst, u, s) void vpdpbusd(int *dst, const uint8_t *u, const int8_t *s) { for (int i = 0; i < 16; i++) { int sum = dst[i]; for (int j = 0; j < 4; j++) { sum += s[i * 4 + j] * u[i * 4 + j]; } dst[i] = sum; } }
従来のAVX-512では同じことを実現するにはvpmaddubsw, vpmaddwd, vpadddの3命令が必要でした。 jit_avx512_core_gemm_s8u8s32_kern.cpp ではどちらのCPUにも対応できるよう次のようにしています。
// Use vpdpbusd if VNNI available, otherwise emulate. void jit_avx512_core_gemm_s8u8s32_kern::dot_product(const Xmm &dst, const Xmm &src1, const Xmm &src2) { if (vnni) vpdpbusd(dst, src1, src2); else { vpmaddubsw(dp_scratch, src1, src2); // [a0 b0 + a1 b1:a2 b2 + a3 b3:...] vpmaddwd(dp_scratch, ones, dp_scratch); // [a0 b0 + a1 b1 + a2 b2 + a3 b3:...] vpaddd(dst, dst, dp_scratch); } }
これにより3倍の性能が得られるそうです(Intel AVX512-Deep Learning Boost: Intrinsic Functions)。 こんな計算が1命令、1クロックサイクルでできるんですね……
畳み込み
2個の同じ大きさ行列A, BがあったときAとBの畳み込みA*Bとは、行と列の同じ位置にある要素同士を掛けて全て足したものです(行列を連続する1次元ベクトルとみなしたときの内積)。
画像認識などでは大きな行列Aと小さな行列Bに対して、Aの左上からBと同じ大きさの部分行列A'を取り出して畳み込みA'*Bを求め、 次にそのとなりの部分行列とBの畳み込み, ...と値を並べて新しい行列を作る操作がよく行われます。

薄いグレーの3x3とBとの畳み込みが[[0, 0, 0], [2, 1, 1], [0, 1, 1]] * B = 3。 点線で囲まれた3x3とBとの畳み込みが[[1, 1, 0], [1, 2, 0], [1, 1, 1]] * B = 4です。
素直な実装はそれほど難しくないのですが、メモリアクセスが飛び飛びになりSIMD化しづらいし遅いです。 そのため行列Aをシーケンシャルアクセス可能なより大きな行列に置き換え、BLASなどの行列演算ライブラリで処理する方法(im2colなど)がよく使われます。
行列の積の高速化についてはw_oさんによる最内ループからはじめる深層学習 (waifu2xの高速化) や いまどきのmatmul がとても勉強になります。
MKL-DNNではカスタム化されたsgemmを実装しています。
キャッシュコントロール
大容量だけど遅いDRAMの一時的な代用領域としてキャッシュメモリが使われます。 CPUに近い側から順にL1, L2, L3というキャッシュメモリがあります。 MKL-DNNではキャッシュサイズなどに応じて細かな制御をします。
prefetchとは指定したアドレスのメモリをキャッシュに読み込ませる命令です。 たとえば、今ある計算をしてからXのメモリを読むと分かっているとします。 そのときprefetch(X)を先に発行しておくと、計算している間にXの値がキャッシュに読み込まれて、実際にmovを実行したとき高速に動作します。 どれぐらい前にprefetchしておくべきかはキャッシュのサイズや速度によって変わります。
たとえばWinogradというアルゴリズムの実装 jit_avx512_common_conv_winograd_kernel_f32.cpp では、キャッシュサイズに応じてprefetch命令の挿入すべき間隔を求めています。
/* assumption: when fetch in Li, data is already in L(i+1) */ int cache_latency; switch (cache_type_) { case L1: cache_latency = 14; break; case L2: case L3: default: cache_latency = 250; break; } prefetch_distance_ = div_up(cache_latency, nb_cache_lines_to_prefetch_);
このL1, L2のレイテンシはXeon-SPの値なんですかね。
そしてこのprefetch_distance_やキャッシュの種類に応じて適切なprefetch命令を挿入するprefetch(int instruction_number)を次のように実装しています。
void prefetch_inst_(const Xbyak::Address &addr) { switch (cache_type_) { case L1: cg_->prefetcht0(addr); break; case L2: cg_->prefetcht1(addr); break; case L3: cg_->prefetcht2(addr); break; default: break; // TODO: raise an exception or put an assert } } void prefetch(int instruction_number) { if (instruction_number % prefetch_spread_ == 0) { for (int i = 0; (i < prefetch_blk_) && (prefetches_issued_ < nb_cache_lines_to_prefetch_); i++, prefetches_issued_++) { prefetch_inst_(cg_->EVEX_compress_addr( reg_base_addr_, (cache_block_size_ * prefetch_distance_) * sizeof(data_t) + (prefetches_issued_ * 64))); } } }
データの書き込みの際にもキャッシュの状態は変わります。通常書き込んだ値は近いうちに読み込まれると想定されるためキャッシュに入れておくと効率がよいからです。 しかし巨大な行列の計算では書き込んだ値が次読まれるまでにたくさんのデータが読み込まれて、せっかくキャッシュに入った値が使われる前に破棄されることがあります。 それならキャッシュに入れない方がよいです。
事前にそうなることが分かっている場合には通常のvmovupsの代わりにキャッシュを変更しないvmovntpsを使うとよいです。 次のstore_outputという関数ではデータのサイズがL3キャッシュサイズ(LLC_data_size)を超える場合はvmovntpsを使うようにしています。
auto store_output = [=](bool output_is_aligned) {
for (int tile = 0; tile < jcp.dimN_reg_block; tile++) {
Zmm zmm(jcp.zmm_start + tile);
if (output_is_aligned
&& jcp.dimK_nb_block == 1
&& (jcp.dimN * jcp.dimM * alpha * alpha
* sizeof(float) > 2 * LLC_data_size))
vmovntps(zword[reg_dstC + 64 * tile], zmm);
else
vmovups(zword[reg_dstC + 64 * tile], zmm);
}
};
データ処理の方法
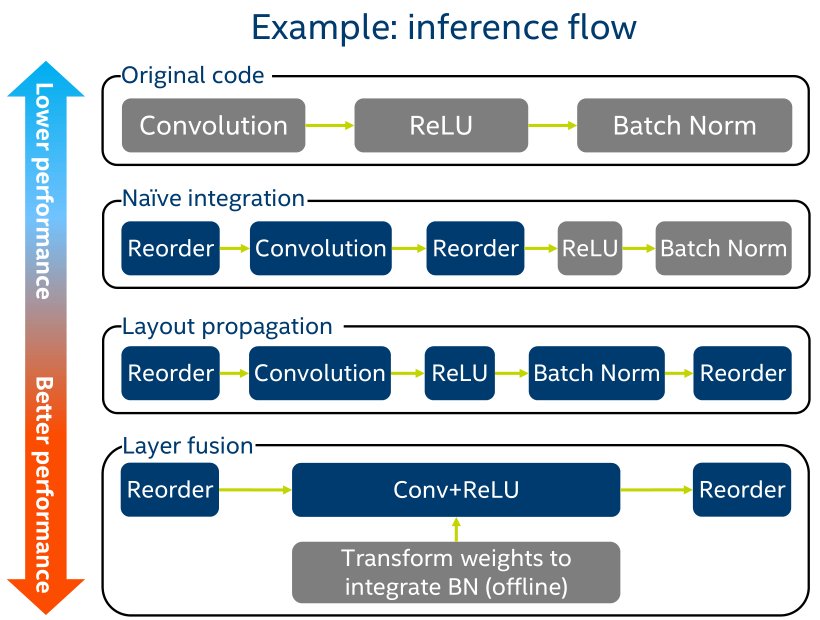
一般的にDNNの学習フェーズでは畳み込み、活性化関数、batch normalizationといった計算を順に行います。 その際それぞれの処理でデータの並び替え(reorder)をします。 ここのメモリアクセスが多く、かつランダムアクセスになりがちなのでMKL-DNNでは畳み込みやそれに続く活性化関数の処理を統合しつつメモリアクセスを減らします。
おわりに
以上、駆け足でしたが気になったテクニックをいくつか紹介しました。
並列プログラミングのためのOpenMPやTBBに、C++のtemplateやラムダ式、そしてむき出しのAVX-512が混在するソースファイルは眺めてるとトリップしそうです。
よくこんな複雑なものを作れるなと感心します。みなさんもぜひごらんになってみてください。 このテキストが少しでも手助けになれば幸いです。